Code generation at a glance¶
The MPC problem description is written in a file called the problem file. The data file for a specific problem is given in a different text file called the data file.
After writing these files, the next step is to actually auto-generate the C code. This is done in two easy steps:
- create an mpc object from the problem file.
- generate code for the data using the newly created mpc object and the data file.
The first step will automatically generate the C-code for the problem. The second step will generate code for the data for two cases: static memory allocation and dynamic memory allocation. In the first case, the data consists on several C files that statically allocate memory and need to be compiled. In the second case, a single data file in json format is written. This data contained in the json file that can be dynamically loaded. The first case (C-code) is useful for deployment in embedded systems, whereas the second case (json file) allows more flexibility during simulation (no need to compile the data).
A basic MPC problem¶
The code generation described in this section basically consist of the following steps:
- write the problem file with the MPC problem description,
- write a data file corresponding to the problem,
- create a
muaompcobject out of that problem, and - create data from that object based on the data file.
The simplest problem that can be setup with the ldt module is an input
constrained problem. The code for this example can be found inside the
tutorial directory muaompc_root/examples/ldt/tutorial,
where muaompc_root is the path to the root directory where
muaompc sources were extracted.
The MPC setup description¶
Consider the following setup. The plant to be controlled is described by the
prediction model 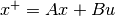 , where
, where
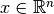 , and
, and 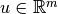 are the
current state and input vector, respectively. The state at the next
sampling time is denoted by
are the
current state and input vector, respectively. The state at the next
sampling time is denoted by 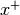 .
The discrete-time system and input matrices are denoted as
.
The discrete-time system and input matrices are denoted as
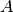 and
and 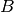 , respectively.
, respectively.
The inputs are constrained to be in a box set 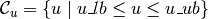 .
.
The MPC setup is thus as follows:
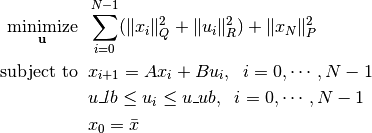
where the integer  is the prediction horizon. The symmetric matrices
is the prediction horizon. The symmetric matrices
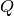 ,
, 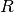 , and
, and 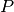 are the state, input, and final state weighting matrices,
respectively. The vector
are the state, input, and final state weighting matrices,
respectively. The vector  represents the system state at the current sampling time, which is given online as a parameter to the optimization problem.
represents the system state at the current sampling time, which is given online as a parameter to the optimization problem.
The optimization variable 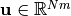 is defined as the sequence
is defined as the sequence  .
Similarly, we define the (auxiliary) state sequence
.
Similarly, we define the (auxiliary) state sequence 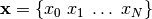 , with
, with 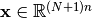 .
.
The MPC problem file¶
The MPC setup can be rather intuitively described in the problem file. In your favorite text editor write the following:
variable u[0:N-1](m);
auxs x[0:N](n);
parameters x_bar(n);
minimize sum(quad(x[i],Q)+quad(u[i], R), i=0:N-1)+quad(x[N],P);
subject to x[i+1] = A*x[i]+B*u[i], i=0:N-1;
u_lb <= u[i] <= u_ub, i=0:N-1;
x[0]=x_bar;
Save the file as myprb.prb.
The resemblance of this file to the mathematical description should be apparent.
Let us make a few remarks about the notation.
The problem description is based on sequences, which are defined
using the format }](_images/math/41050153b0b9f33ab38271a24acbfbdac1a6e943.png) , where
, where  is the name of the
sequence,
is the name of the
sequence, 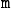 is the length of each vector in the sequence, and
is the length of each vector in the sequence, and  and
and 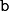 denote the index of the first and last element of the sequence.
To refer to the element
denote the index of the first and last element of the sequence.
To refer to the element 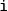 of this sequence, we use the notation
of this sequence, we use the notation ![\texttt{v[i]}](_images/math/c30933103166297db39924d22b23370321d0a2c8.png) .
In the case that a sequence consist of a single element, only the vector length need
to be specified, i.e.
.
In the case that a sequence consist of a single element, only the vector length need
to be specified, i.e. 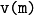 .
To refer to this vector no indexing is required in later parts of the problem specification,
i.e. it suffices to write
.
To refer to this vector no indexing is required in later parts of the problem specification,
i.e. it suffices to write  .
.
The 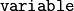 keyword identifies the optimization variable.
The
keyword identifies the optimization variable.
The  keyword identify sequences that are to be specified
online.
The keyword
keyword identify sequences that are to be specified
online.
The keyword 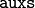 is used to specify the dimensions of the sequence
is used to specify the dimensions of the sequence  .
.
The keyword 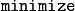 identifies the text following it as the cost function to be minimized. Several
special keywords are accepted, for example the
identifies the text following it as the cost function to be minimized. Several
special keywords are accepted, for example the ![\texttt{sum(h[i], i=a:b)}](_images/math/53a927c4b41501cf571babcedc7f5ae029086ccc.png) denotes the summation of the
real valued functions
denotes the summation of the
real valued functions 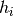 for
for 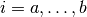 . The keyword
. The keyword 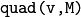 denotes the quadratic form
denotes the quadratic form 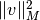 .
.
As seen in problem file, the
equality and inequality constraints
follow after the keyword 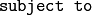 .
The constraints optionally accept an index variable and its range.
For example, the prediction model is written as
.
The constraints optionally accept an index variable and its range.
For example, the prediction model is written as ![\texttt{x[i+1] = A*x[i] + B*u[i], i=0:N-1}](_images/math/63d777e3116df4c811cb9ef4752df76d4cd74245.png) .
.
With the problem file already finished, we can now write the data file.
The MPC data file¶
The data file must contain the numerical values for the matrices, vectors,
and scalars found in the problem file.
Values for the sequences defined by the keywords
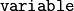 ,
,  and
and 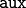 are not required.
Thus, in our example, values for
are not required.
Thus, in our example, values for 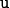 ,
,  ,
and
,
and  do not need to be specified.
The following elements need to be specified:
the matrices
do not need to be specified.
The following elements need to be specified:
the matrices
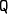 ,
, 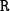 ,
, 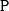 ,
,
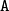 ,
, 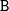 ,
the vectors
,
the vectors
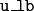 ,
, 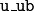 ,
and the scalars
,
and the scalars
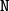 ,
, 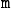 ,
, 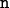 .
.
The matrices are specified using MATLAB syntax. For example, an identity matrix 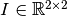 could be written in the following ways:
could be written in the following ways:
I = [1 0; 0 1]
I = [1, 0; 0, 1]
Without going into further details, let us write data file. In your favourite text editor write:
# weighting matrices
Q = [1, 0; 0, 1]
R = [1]
P = [1, 0; 0, 1]
# system matrices
A = [1., 0.01; 0., 0.9]
B = [1.e-04; 0.02]
# input constraints
u_lb = [-100]
u_ub = [100]
# dimensions
N = 5
n = 2
m = 1
Save this file as mydat.dat.
The matrices 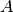 and
and 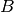 represent the discrete time model of a DC-motor.
The state vector is given by
represent the discrete time model of a DC-motor.
The state vector is given by ![x = [x_1 \; x_2]^T \in \mathbb{R}^n](_images/math/30cbb7dad7e32610956be72f518980012004eab0.png) , where
, where  and
and 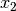 are the rotor
position and angular speed, respectively. The input is
constrained to be between -100% and 100%.
are the rotor
position and angular speed, respectively. The input is
constrained to be between -100% and 100%.
For this example, we chose the weighting matrices to be
identity matrices of appropriate size, i.e. 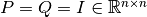 , and
, and 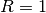 .
Clearly, the value of dimension of the state and input vector are
.
Clearly, the value of dimension of the state and input vector are
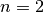 and
and 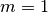 .
The horizon length is specified as steps through the parameter
.
The horizon length is specified as steps through the parameter 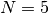 .
.
Generating the C-code¶
Now that we have written the myprb.prb problem file,
we proceed to create an mpc object.
In the directory containing myprb.prb,
launch your Python interpreter
and in it type:
from muaompc import ldt
mpc = ldt.setup_mpc_problem('myprb.prb')
This will generate code specific for the problem described
by myprb.prb.
By itself, the code we just generated is very not useful.
It only contains and abstract description of an MPC problem
without any data.
The next step is to generate code for data
that can be used with the problem code
for myprb.prb we just generated.
To generate code that represents the data in mydat.dat,
continue typing in your Python interpreter:
ldt.generate_mpc_data(mpc, 'mydat.dat')
And that’s it! If everything went allright, you should now see inside current
directory a new folder called myprb_mpc. As an alternative to typing the
above code,
you can execute the file main.py found in the tutorial directory,
which contains exactly that code. The tutorial directory already contains
the files myprb.prb and mydat.dat.
In the next section, you will learn how to use the generated C code.
Tip
If the code generation was not succesful, try passing the verbose=True
input parameter to the function setup_mpc_problem. It will print extra
information about the code generation procedure. For example:
mpc = ldt.setup_mpc_problem('myprb', verbose=True)
Tip
By default, the generated code uses double precision float (64-bit) for all
computations. You can specify a different numeric representation via
the input parameter numeric of the function setup_mpc_problem.
For example, to use single precision (32-bit) floating point numbers type:
mpc = ldt.setup_mpc_problem('myprb.prb', numeric='float32')
Using the generated code¶
In the folder myprb_mpc you will find all the automatically
generated code for the current example.
To use the generated code in a control loop, the following steps are to be followed:
- setup a MPC controller
- configure the optimization algorithm
- set the parameters for the MPC controller
- solve the MPC problem
- apply the control input
- repeat from step 3
We now proceed to exemplify the use of the generated code from steps 1 to 5. We start our tutorial using the MATLAB interface, as it is simpler to explain. Later we show how it is done in pure C.
Note
The Python interface to the generated C-code will be available in future releases.
Using the generated code in MATLAB¶
The MATLAB interface makes it possible to directly make of the generated code and data (i.e. the MPC controller) from within MATLAB.
Once the code has been generated, the next step is to compile the MATLAB interface.
Start MATLAB, and switch to the folder
myprb_mpc/src/matlab.
In the MATLAB console type mpcmake, which will execute the mpcmake.m script.
The last step is to add the matlab directory to the PATH environment in
MATLAB.
For example,
assuming the MATLAB current directory is
the tutorial directory muaompc_root/examples/ldt/tutorial, in the MATLAB console type:
cd myprb_mpc/src/matlab
mpcmake
cd ..
addpath matlab
Now you can use the interface which is encapsulated in a class called
mpcctl which represents the MPC controller. Simply declare an
instance of that class, which we usually call ctl (controller).
The input parameter for the constructor of the class is the name
of a json file contaning the generated data.
muaompc by default saves the data in the folder
myprb_mpc/data/mydat. In our example,
the generated json data file is called mpcmydat.json.
Continue typing in the console:
ctl = mpcctl('myprb_mpc/data/mydat/mpcmydat.json');
The next step is to configure the optimization algorithm. In this case, we have an input constrained problem. The only parameter to configure is the number of iterations of the algorithm (see section Tuning for details). For this simple case, let’s set it to 10 iterations:
ctl.conf.in_iter = 10;
Let us assume that the current state is ![\bar{x} = [0.1 \; -0.5]^T](_images/math/86f6e70b1766a3da420f81ecabf0d4f8bcff08e6.png) .
The controller object has a field for the parameters defined in the problem file. The parameter
.
The controller object has a field for the parameters defined in the problem file. The parameter x_bar can be set as follows:
ctl.parameters.x_bar = [0.1; -0.5];
We can finally solve our MPC problem for this state by calling:
ctl.solve_problem();
The solution is stored in an array ctl.u_opt, whose first 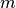 elements are
commonly applied to the controlled plant.
The complete MATLAB example can be found in the tutorial folder under
elements are
commonly applied to the controlled plant.
The complete MATLAB example can be found in the tutorial folder under main.m.
Using the generated code in C¶
The folder myprb_mpc/data/mydat already contains a template
for a main file, called mpcmydatmain.c.
Switch to the the folder mydat and open mpcmydatmain.c
in your favourite editor.
This template file shows how to solve an MPC problem using dynamic
or static memory allocation.
This file might look at bit daunting at first, but it just a template
you can modify to fit your needs.
In the current directory you will find two main files with just the basics,
that are based on the template file.
The file mpcmydatmain_dynmem.c exemplifies how the dynamic memory allocation
is done in C code. The file mpcmydatmain_staticmem.c exemplifies the
how the static memory allocation version of the data can be used.
Both files follow the same structure as the MATLAB
tutorial above.
Let us take the file mpcmydatmain_staticmem.c as example.
The first thing to include
is the header file of the library called mpcctl.h.
We need to have access to some of the algorithm’s variables, for example the MPC
system input, the parameters, and the algorithm settings. This is done through the fields of the
struct mpc_ctl structure, which we denote the controller structure.
We first create an instance of this controller structure, and we set the controller by passing a pointer to the structure to the function mpcmydat_ctl_setup_ctl, which is found in mpcmydatctldata.h.
For example, after including the corresponding headers, in the body of the main function we type:
struct mpc_ctl ctlst; /* Structure for static memory allocation */
struct mpc_ctl *ctl; /* pointer to the an allocated structure */
ctl = &ctlst;
mpcmydat_ctl_setup_ctl(ctl);
Once we controller is setup, we can continue in a similar fashion to the MATLAB case, that is first we setup the parameters, then we configure the algorithm, solver the problem:
ctl->parameters->x_bar[0] = 0.1;
ctl->parameters->x_bar[1] = -0.5;
ctl->solver->conf->in_iter = 10;
mpc_ctl_solve_problem(ctl);
Finally, the computed control input is found in the array ctl->u_opt.
Note
At the moment the user needs to know the length of the different arrays in the controller structure. This information can be infered by the user from the problem and data files. The length of the different arrays will be available in the controller structure in future releases.
To run an compile this code do the following. Copy the file mpcmydatmain_staticmem.c into the folder myprb_mpc/data/mydat and remove the main template file mpcmydatmain.c found in myprb_mpc/data/mydat (otherwise you will end up with two main functions in two different files, and the compilation will fail). In that folder you will also find example
Makefiles, called mpcmydatMakefile.*, which compiles the
generated code.
The Makefile mpcmydatMakefile.mk compiles the code
using the GNU Compiler Collection (gcc).
Adapt the Makefile to your compiler if necessary.
For example, to generate, compile and run the code in Linux you would type in a console:
cd muaompc_root/examples/ldt/tutorial # the tutorial folder
python main.py # generates code and data
cp mpcmydatmain_staticmem.c myprb_mpc/data/mydat # the tutorial main file
cd myprb_mpc/data/mydat
rm mpcmydatmain.c # remove template main file
make -f mpcmydatMakefile.mk # compile
./main # run the controller
If everything went okay, you will see the output:
ctl->u_opt[0] = 3.056814e-02
This concludes our tutorial!
Where to go next¶
In the folder muaompc_root/examples/ldt/ you will find further examples.